Please find the attachment for a complete understanding of the solution provided here.
As can be seen from the diagram, the hypotenuse, LM is 76 and the base, MN is 40. We have to find the angle M.
From basic trigonometry we know that

Thus, in our case, we will have,
 as
as
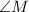 and thus, the above equation will modify as:
and thus, the above equation will modify as:
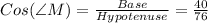
Therefore,
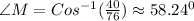
Thus out of the given options, option D is the closest to the answer we got.