The answers are 3.19 or -2.19.
In order to complete the square, you must first get the constant to the other side of the equation. WE do that by adding 7 to both sides.
x^2 - x - 7 = 0
x^2 - x = 7
Now we must take half of the x coefficient (-1), which would be -.5. Then we square it and add it to both sides. This is the second step to any completing the square problem.
x^2 - x = 7
x^2 - x + .25 = 7.25
Now that we have done that, the left side will be a perfect square so that, we can factor it.
x^2 - x + .25 = 7.25
(x - .5)^2 = 7.25
After having done that, we can take the square root of both sides
(x - .5)^2 = 7.25
x - .5 = +/-
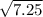
Now we can take the value of that square root and solve.
x - .5 = +/-
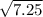
x - .5 = +/-2.69
x = .5 +/- 2.69
And with the + and - both there, we need to do both to get the two answers.
.5 + 2.69 = 3.19
.5 - 2.69 = -2.19