Question

Geometry . Cosines / sines. Find a and round to the nearest 10th

Answer 1

This is the good part of Trigonometry, actually measuring triangles. It's much better than all the identities around sine and cosine and the rest, which actually have more to do with circles than triangles.

This part of trig has a short menu:

Law of Cosines. Three ways to write it, one is
`c^2 =a^2+b^2-2ab \cos C`

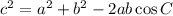
Law of Sines:
`(a)/(\sin A) = (b)/(\sin B) = (c)/(\sin C)`

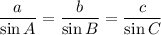
Triangle angles:
`A+B+C=180^\circ`

and two special cases of the Law of Cosines, the Pythagorean Theorem

`C=90^\circ, \quad \quad c^2=a^2+b^2`

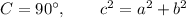
and the Collinear Points Theorem:

`C=180^\circ, \quad \quad c^2=a^2+b^2 - 2 a b \cos 180^\circ = a^2+b^2+2ab=(a+b)^2`

`c = a+b`

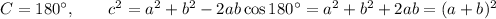
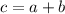
Here we choose Triangle Angles followed by Law of Sines:

A = 180 - 105 -15 = 60 degrees

`(a)/(\sin 60^\circ)= (2)/(\sin 105^\circ)`

`a= (2 \sin 60^\circ)/(\sin 105^\circ) = 1.793...`

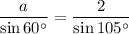
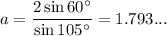
Answer: 1.8 cm

When I was a student we'd be expected to get
`\sin 105^\circ` exactly and get

`a = 3 √(2) - \sqrt 6`

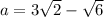
But that was before online homework.