Question

The ratio of the numerator to the denominator of a certain fraction is one to four. If three is added to the numerator and subtracted from the denominator, the new fraction reduces to one-third. What is the original fraction?

Answer 1

Let x = the numerator part of the original fraction. Since the ratio of the numerator to denominator is one to four, this means 4x is the denominator.

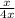`(x)/(4x)` is our original fraction.

Now we work with adding and subtracing to get to something that looks like one-third.

`(x+3)/(4x-3) = (x)/(3x )`

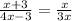
We write the second half as x / 3x because the fraction can simplify to 1/3. The rest of the problem is solved by cross multiplying (essentially, clearing fractions and simplifying) and solving for x.

`(x+3)/(4x-3) = (x)/(3x )`

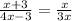
(3x)(x + 3) = (4x -3)(x)

3x² + 9x = 4x² - 3x

Since it's a quadratic, let's set one side equal to zero and use the Zero Product Property (ZPP).

9x = x² - 3x

0 = x² - 12x

x is a common factor in x²-12x, so we can use the ZPP and factor

0 = x (x - 12)

So x = 0 or x =12.

Having zero as an answer won't work as we'd be dividing by zero. Let's check x = 12.

12/48 is the starting fraction, which simplifies to 1/4

12+3 / 48 -3 = 15 / 45 = 1/3.

Thus, 12/48 was the starting fraction.

Answer 2

Answer: The required original fraction is
`(12)/(48).`

Step-by-step explanation: Given that the ratio of the numerator to the denominator of a certain fraction is one to four.

Also, if three is added to the numerator and subtracted from the denominator, the new fraction reduces to one-third.

We are to find the original fraction.

Let x and y represents the numerator and denominator of the original fraction.

Then, according to the given information, we have

`x:y=1:4\\\\\Rightarrow (x)/(y)=(1)/(4)\\\\\Rightarrow y=4x~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

and

`(x+3)/(y-3)=(1)/(3)\\\\\Rightarrow 3(x+3)=1(y-3)\\\\\Rightarrow 3x+9=y-3\\\\\Rightarrow 3x+9=4x-3~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~[\textup{using equation (i)}]\\\\\Rightarrow 4x-3x=9+3\\\\\Rightarrow x=12.`

From equation (i), we get

`y=4*12=48.`

Thus, the required original fraction is
`(12)/(48).`