Question

If the measure of a tangent-chord angle is 68 degrees, then what is the measure of the intercept arc inside the angle

A.112

B.68

C.34

D.136

Answer 1

The answer to this is D!

Hope I helped

Answer 2

Please find the attached diagram for a better understanding of the question.

For solving this question we will make use of a theorem which says: Tangent-chord angles are equal to half the measure of the intercepted arc.

Thus, if we use this theorem in our diagram, we will arrive at this equation:-

`m \angle PRS= (1)/(2) m\angle PQR`

Now, we are given that
`m\angle PRS=68^(0)` (please note that
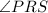`\angle PRS` is the angle between the tangent and the chord.)

Therefore,
`m\angle PQR=2* (m\angle PRS)`

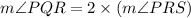
Thus,
`m\angle PQR=2* 68^(0)`

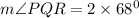
Or
`m\angle PQR=136^(0)`

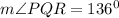
Therefore, we conclude that Option D is the correct answer.