Question

What is the measure of the angle labeled (5x+42)° ?

Answer 1

We see two parallel lines crossed by a transversal.

The two labelled angles are alternate interior angles, hence they are equal.

The equality allows us to equate the two expressions and hence solve for x.

8x-3=5x+42

transpose terms

8x-5x=42+3

solve for x

3x=45

so x=45/3=15.

This means 5x+42=5*15+42=75+42=117 degrees.

Answer 2

These angles are known as alternate interior angles. A fact about them is that they are always congruent. Since they are congruent, we can set them equal to each other:

`8x-3=5x+42`

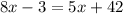
Let's find the value of x so that we can find what (5x + 42) is:

`8x-3=5x+42`

`8x=5x+45`

`3x = 45`

`x = 15`

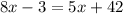
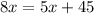
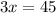
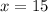
x = 15 so we can plug that in to find the angle:

`5(15)+42 = 75+42 = 117`

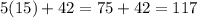
Thus, that angle is equal to 117°.