Question

What is the square root for √84?
Simplified and the non simplifed one

Answer 1

•Simplified Square Root for √84 is 2√21
√4*21=√84.
Now extract and take out the square root √4 * √21. Root of √4=2 which results into 2√21

•Determine the square root.
The square root of eighty-four √84 = 9.16515138991

Answer 2

To simplify the square root, find the prime factorization of the number within the square root:

`84 = 7 * 12`

`7 * 12 = 7 * 4 * 3`

`7 * 4 * 3 = 7 * 2 * 2 * 3`

`√(84) = √(2 * 2 * 3 * 7)`

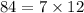
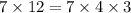
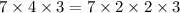
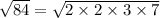
Take any number that is repeated twice within the prime factorization, and move it outside of the root:

`√(2 * 2) = 2`

`√(2 * 2 * 3 * 7) = 2 √(3 * 7) = \boxed{2 √(21)}`

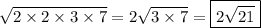
The simplified form of √84 will be 2√21.

The non-simplified form is found by putting the term into the calculator:

`√(84) = \boxed{9.166}`

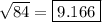
Rounded to the nearest thousandths place, the non-simplified form of √84 will be 9.166.