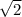Question

Geometry.Find the indicated side of the triangle. Include a clear answer and description if possible

Answer 1

In this problem we are given a right triangle with 45 degree angle. We know that the sum of a triangle's angles needs to be equal to 180 degrees.

When we subtract 90+45 from 180 we got 45. That means we have an isoceles triangle.

According to the Pythagorean Theorem,
`a^(2) +b^(2) =c^(2)` .

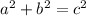When we plug in the numbers we get:
`a^(2) +b^(2) =10^(2)`

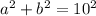
Because we know that a = b, we can write this as:
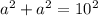`a^(2) +a^(2) =10^(2)` or
`2a^(2) =10^(2)`

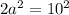
Simplify:
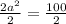`(2a^(2))/(2) =(100)/(2)`, then
`a^(2) =50`

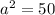
Take the square root:
`\sqrt{a^(2)} =√(50) =>a=5√(2)`

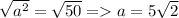
So, B is
`5√(2)`

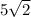
To find it faster we have a formula for this: "If a right triangle has 2 equal angles, the hypotenuse is equal to
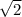`√(2)` times the leg."

Vice-versa: leg ×
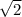`√(2)` = hypotenuse or leg = hypotenuse /
`√(2)`