To prove this, I solved for the answer, to see if there was a pair of natural numbers that fit.
ab=22+ \frac{4-a-b}{6}
6ab = 132 + 4 - a - b
6ab = 136 - a - b
We know that an even # times an even # is even, odd times odd is odd, and odd times even is even, but even minus an odd number minus an even number is odd. So if a and b are even, then the result is even, if they're odd, then multiply by 6, they become even, and an even minus an odd minus an odd becomes even again. Basically, a and b must both either be even or both be odd.
Another thing is that ab ≤ 22, because if we try to keep
(4-a-b)/6
positive, the only posible numbers are 0, 1, 2, 3, and 4, and plugging them in doesn't give us the answer, so
(4-a-b)/6
must come out negative, which means ab must be smaller than 22.
Knowing this, I guessed through a list of numbers, and the numbers 7 & 3 go into the equation and come out right.
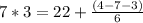
21 = 22 + (-6/6)
21 = 22 - 1
21 = 21
7 and 3 are natural numbers.