The answer is:
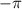
The explanation for this exercise is shown below:
1. By definition, a rational number can be written as a fraction, whose numerator and denominator are integers. The irrational numbers can't be written as a fraction.
2.
 is an irrational number, because you can't write it as a fraction. The only way to get a rational number with the sum of
is an irrational number, because you can't write it as a fraction. The only way to get a rational number with the sum of
 and other irrational number shown in the image attached, is that this number added be
and other irrational number shown in the image attached, is that this number added be
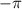 , because
, because
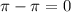 and
and
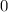 is a rational number.
is a rational number.