Answer: The correct option is (A). 464 square units.
Step-by-step explanation: We are given a rectangle inside a regular hexagon in the figure.
We know that each side of a regular hexagon has same measure, so the measure of each side is
a = 18 units.
Therefore, the area of the regular hexagon is given by
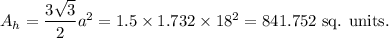
Since the rectangle has length and breadth of 21 units and 18 units respectively, so the area of the rectangle is
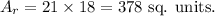
Thus, the area of the shaded region in the figure will be

Hence, option (A) is correct.