Question

Find the equation of the circle that has a diameter with endpoints located at (-3,6) and (9,6)

Answer 1

The endpoints of the diameter give us two crucial hints:

1) The length of the radius if half the length of the diameter (and we can compute it knowing its endpoints)

2) The center of the circle is the midpoint of the diameter (and we can compute it knowing its endpoints)

So, the length of the diameter is the distance between its endpoints, which we can easily compute since their y coordinate is the same: the distance is the absolute difference between the x coordinates, so

`d = |-3-9| = |-12| = 12`

Which means that the radius is 6 units long.

As for the midpoint (i.e. the center of the circle), its x coordinate is the average of the x coordinates of the endpoint:

`\cfrac{-3+9}{2} = \cfrac{6}{2}=3`

while its y coordinate will obviously be 6, since both endpoints have the same y coordinate.

Recap: we know the center and the radius of the circle:

`C = (3,6),\qquad r = 6`

Everytime you know the center
`(x_0,y_0)` and the radius
`r` of a circle, you can write its equation as

`(x-x_0)^2 + (y-y_0)^2 = r^2`

Plug your values to get

`(x-3)^2 + (y-6)^2 = 36`

Answer 2

To find the equation of a circle that has a diameter with endpoints located as (-3,6) and (9,6), the first step is to find the radius. But, before we do that, we have to find the diameter.

Since both of these coordinates have the same y coordinate, that means we just have to subtract the x coordinates to find the diameter. 9 - (-3) is 12, so the diameter is 12.

Now to find the radius. Since the radius is 1/2 of the diameter, the radius here is 12 * 1/2 = 6.

The next step is to find the center of the circle. We can do that by finding what point is at the center of the endpoints we know. We can do this by find the midpoint of that segment, which we can do by using the midpoint formula. We need to take the averages of each of the x and y coordinates. For y, it will be 6 (because the y is the same in both points). Now for the x:

`(-3+9)/(2) = 3`

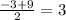
That means that that the center of the circle is (3, 6). Now we can start to make the equation.

The equation of a circle with center (h, k) and radius r is:

(x - h)² + (y - k)² = r²

Now we can substitute our values and get the equation. The equation is:

(x - 3)² + (y - 6)² = 36