Question

At 10 a. m. two classmates start out on their bikes to meet each other from towns located 68 miles apart. At 1:00pm they meet. If one boy traveled 3 miles per hour faster than the other, what was the rate of speed of each boy?

Answer 1

Let, the rate of speed of one boy be r miles per hour.

So, the speed of other boy be (r+3) miles per hour.

The two boys start out at 10 a.m. and 1 p.m. they meet. So they travel for 3 hours.

We will find the miles they had travelled in 3 hours.

One boy travels in 1 hour = r miles.

So in 3 hours he will travel = (3r) miles

Similarly the other boy will travel in 3 hours = 3(r+3) miles = (3r+9) miles.

Given, the total distance they had travelled is 68 miles.

So we can write the equation,

`3r+(3r+9) = 68`

`3r+3r+9 = 68`

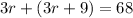
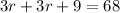
Now we will add like terms. here like terms means r with r. So we will add 3r and 3r.

`6r+9 = 68`

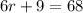
Now we will move 9 to other side by subtracting it from both sides.

`6r+9-9 = 68-9`

`6r = 68-9`

`6r = 59`

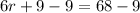
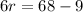
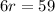
We can get r from 6r, by dividing 6 to both sides.

`6r/6 = 59/6`

`r = 59/6`

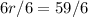
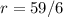
So we have got the rate of speed for one boy that is

59/6 miles = 9 5/6 miles

The rate of speed of the other boy

= (r+3) miles per hour

= (9 5/6 + 3) miles per hour

= 12 5/6 miles per hour

So we have got the required answer.

Rate of speed of one boy = 9 5/6 miles per hour and the other boy

= 12 5/6 miles per hour