Question

An arithmetic sequence has the terms a6=53 a 6 = 53 and a8=61 a 8 = 61 . Questions: What is the value of d d ? AnswerIncorrect What is the value

Answer 1

The given terms are two terms apart, so their difference is twice the difference of adjacent terms.

`a_8-a_6=2d=61-53=8\\\\d=(8)/(2)=4`

The value of d is 4.

Answer 2

The value of d is 4.

Explanation:

It is given that the 6th term of an AP is
`a_6=53` and 8th term is
`a_8=61`.

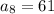The nth term of an AP is

`a_n=a+(n-1)d`

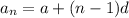
6th term of an AP is
`a_6=53`.

`a_6=a+(6-1)d`

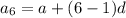
`53=a+5d` .... (1)

8th term is
`a_8=61`.

`a_8=a+(8-1)d`

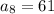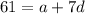`61=a+7d` .... (2)

Subtract equation (1) from equation (2).

`61-53=a+7d-(a+5d)`

`61-53=a+7d-a-5d`

`8=2d`

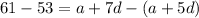
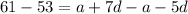
Divide both sides by 2.

`4=d`

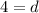
Therefore the value of d is 4.