We have vertex form for parabola equation as
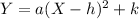
where (h,k) is the vertex.
As the turning point given here is (2,1) so thats the vertex.
On comparing (2,1) with (h,k), we can see
h = 2, k = 1
Plugging 2 in h place and 1 in k place in
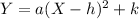 we get
we get
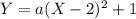 ------------------------ (1)
------------------------ (1)
Now we need to find value of a.
For that we will use point (0,5) given on parabola.
On comparing (0,5) with point (X,Y) we get X = 0, Y = 5
so plug 0 in X place and 5 in Y place in equation (1)
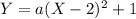
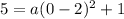
Simplify and solve for a as shown
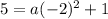
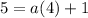
5 -1 = a(4) + 1 - 1
4 = a(4)
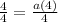
1 = a
Now plug 1 in a place in equation (1) as shown
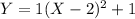
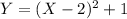
So thats the vertex equation of parabola and final answer.