Question

Cosines someone please help me. Include an explanation and a clear answer

Answer 1

The law of cosines states that, if you know two sides of a triangle and the angle between them (let's call them
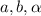`a,b,\alpha`, then the third side
`c` is given by the following formula:

`c^2 = a^2+b^2-2ab\cos(\alpha)`

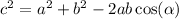
You may have noticed that this formula strongly resembles the Pythagorean theorem. In fact, this is a generalization, since the Pythagorean theorem only works for right triangles, where the cosine part is zero and vanishes.

Anyways, plugging the values from your particular case we have

`c^2 = 49+64-2\cdot7\cdot8\cos(32) \approx 18.02`

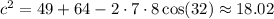
This means that
`c = √(18.02) \approx 4.24`

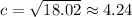
Which rounded to the nearest tenth gives 4.2

Answer 2

The formula for the law of cosines is:

a^2 = b^2 + c^2 - 2*b*c*cos(angle)

In this triangle b = 7, c = 8 and angle = 32.

a^2 = 7^2 + 8^2 - 2*7*8*cos(32)

a^2 = 18.018

a = SQRT(18.018)

a = 4.24

C = 4.2 feet.