Question

a missile is launched from the ground. its height, h(x), can be represented by a quadratic function in terms of time, x, in seconds. 130 after 1 second, the missile is 103 feet in the air; after 2 seconds, it is 240 feet in the air. find the height, in feet, of the missile after 11 seconds in the air. help!

Answer 1

The height of the missile in the air after 11 seconds is 330 feet.

Explanation:

The standard form for the quadratic function f(x)=
`ax^2 + bx + c`, which is the function of the parabola model.

We are given two points.

(1, 130) and (2, 240)

Here the first coordinate represents the x (time) and the second coordinate represents h(x), which is height.

Now plug these two coordinates and find the two equations.

(1, 130), the equation is

130 = a.(1)^2 + b(1) + c, where "c" is the initial height. Which is equal to zero.

Therefore, we get

130 = a + b + 0

a + b = 130 -------(1)

Now let's form the second equation using the coordinate (2, 240)

240 =
`a(2)^2 + b(2) + 0`

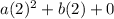
240 = 4a + 2b -------------(2)

Now let's solve the equations (1) and (2) and find the value of "a" and "b"

a + b = 130 can be written as a = 130 - b

Here we can use the substitution method.

Now plug in a = 130 - b in the second equation, we get

240 = 4(130 - b) + 2b

240 = 520 - 4b + 2b

240 = 520 - 2b

2b = 520 - 240

2b = 280

Dividing both sides by 2, we get

b = 140

Now plug in b = 140 in a = 130 -b and find the value of a

a = 130 - 140

a = -10

Now we got a = -10 and b = 140.

We plug in a = -10 and b = 140 in the general form, we gety

h(x) =
`-10x^2 + 140x + c`

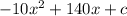
Where c is the initial height, which is equal to 0.

h(x) =
`-10x^2 + 140x`

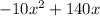
Now plug in x = 11 seconds and find the height.

h(11) = -10(11)^2 + 140 (11)

= -10 (121) + 1540

= - 1210 + 1540

h(11) = 330 feet,

Therefore, the height of the missile in the air after 11 seconds is 330 feet.