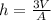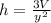Question

The volume of a solid right pyramid with a square base is V units3 and the length of the base is y units what is the height of the pyramid?

Answer 1

Answer:
`h=(3V)/(y^(2) )`

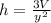
Step-by-step explanation: The volume of a pyramid is equal to one-third the product of the area of the base and the height:

`V=(1)/(3)A*h`

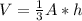
In this case, the base is a square, so its area is:

A=y^2 where "y" is the lenght of the base edge

So isolating the height it would be:

`h=(3V)/(A)`

`h=(3V)/(y^(2) )`

Answer 2

Formulas

V = (1/3)* pi*B*h

B = s*s which is one side of the square base multiplied by itself.

Givens

s = y

V = V

h = ??

Substitute

V = (1/3)s^2*h Multiply both sides by 3

3V = s^2 * h

3V / s^2 = h

But y = s

3V /y^2 = h