Question

A recent survey based on a random sample of n=470 voters, predicted that independent candidate for the mayoral election will get 24% of the vote, but he actually got 27%. discuss whether the claim that suggest the survey was done incorrectly! explain your rational.

Answer 1

I have an expression

`\sigma = √(p(1-p)/n)`

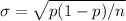
floating around in my head; let's see if it makes sense.

The variance of binary valued random variable b that comes up 1 with probability p (so has mean p) is

`E( (b-p)^2 ) = (-p)^2(1-p) + (1-p)^2p = p(1-p)`

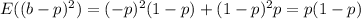
That's for an individual sample. For the observed average we divide by n, and for the standard deviation we take the square root:

`\sigma = √(p(1-p)/n)`

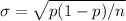
Plugging in the numbers,

`\sigma = √(.24(1-.24)/490) = 0.019 = 1.9\%`

One standard deviation of the average is almost 2% so a 27% outcome was 3/1.9 = 1.6 standard deviations from the mean, corresponding to a two sided probability of a bit bigger than 10% of happening by chance.

So this is borderline suspect; most surveys will include a two sigma margin of error, say plus or minus 4 percent here, and the results were within those bounds.