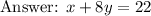Nice. We're not really told which is the right angle. We can tell from the squared distances:
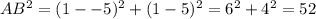
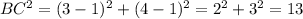
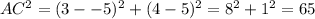
We see
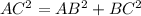 so B is the right angle.
so B is the right angle.
That was preliminary and probably indicated in an associated figure.
Now we want the line through the midpoint of the legs, AB and BC, in standard form.
The midpoint of AB is the average of the coordinates of A and B:
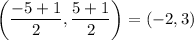
The midpoint of BC is
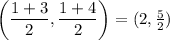
The line through those points is
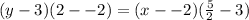
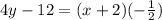
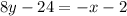
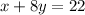
That's the answer. Let's check it.
Midpoint of AB is (-2,3), -2 + 8(3)=22 good.
Midpoint of BC is (2,5/2), 2+8(5/2)=22 good.