Question

A plastic ball has mass M. It floats in water with (1/5)th of its volume under the water line. What downward force must be applied to the ball to submerge it and hold it at rest below the surface of the water

Answer 1

F = -4/5 W

Step-by-step explanation:

We will do this exercise in parts, let's start with the data, The ball must be in balance

B -W = 0

B = mg (1)

where the thrust is given by Archimedes' principle

B = ρ g V_liquid

In the problem we are told that the volume of the submerged body is 1/5 of the volume of the body, let's use the subscript 2 for the ball and the subscript 1 for the liquid

V₁ =
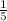`(1)/(5)` V₂

if we use the concept of density for the body

ρ₂ = m / V₂

m = ρ₂ V₂

We can see that mass and volume are directly proportional, so we can use a rule of three to find the submerged mass. If mass M is in volume V₂ what mass is there in volume V₂ /5

m₂ =
`(V_(2) )/(5) (M)/(V_(2) )`

m₂ = M / 5

we substitute in equation 1

B = M / 5 g

This is the thrust that is an upward vertical force, therefore to submerge the whole ball we must apply a downward vertical force equal to the rest of the weight, the equilibrium condition in this case is

B -W - F = 0

F = B -W

F =
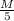`(M)/(5)` g - M g

F = -4/5 Mg

F = -4/5 W

The negative sign indicates that the force is vertical down