Question

Consider the functions f and g defined by f(x) = sqrt((x+1)/(x-1)) and g(x) = (sqrt(x+1)/sqrt(x-1)). explain why f and g are not the same function.

Answer 1

If f(x) and g(x) were the same function, they would produce identical outputs from identical inputs. If we can find a single example where they don't, we've proven that they're distinct.

Take x = 3, for instance. For f(3), we find

`f(3)=\sqrt{(3+1)/(3-1)} =\sqrt{(4)/(2)} =√(2)`

while for g(3):

`g(3)=(√(3+1))/(√(3-1)) =(√(4))/(√(2)) =(2)/(√(2))`

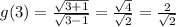
From this example, we can see that we're dealing with two nonequivalent functions.

EDIT: I've realized that I made a pretty big gaffe here, since

`(2)/(√(2)) *(√(2))/(√(2))=(2√(2))/(2)=√(2)`

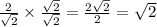
My argument would actually be incorrect in this case, then, and Konrad's would be more appropriate.

Answer 2

By the property
`\sqrt{(a)/(b)}=(\sqrt a)/(\sqrt b )`, it may seem that both functions are the same, but they're not, because they have different domains.

`f(x)=\sqrt{(x+1)/(x-1)}\\(x+1)/(x-1)\geq 0\wedge x\\ot=1\\(x+1)(x-1)\geq0\\x\in(-\infty-1\rangle\cup\langle1,\infty)\\\boxed{D:x\in(-\infty-1\rangle\cup(1,\infty)}\\\\\\g(x)=(√(x+1))/(√(x-1))\\x+1 \geq 0 \wedge x-1\geq 0 \wedge √(x-1)\\ot =0\\x\geq -1 \wedge x\geq 1 \wedge x\\ot =1\\\boxed{D:x>1}`

`D_(f(x))\\ot=D_(g(x))` so the two functions are not the same.