Question

An empty cylindrical vase with a radius of 8 cm and a height of 9 cm is filled with 6 cm^3 of sand every 15 seconds. At the same time 8cm^3 of sand is taken out of the vase every minute. After how many minutes will the base be half filled with sand?

Answer 1

General Idea:

The volume of cylinder is given by
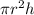`\pi r^(2) h`, where r is the radius and h is the height of the cylinder.

Applying the concept:

Step 1: We need to find the volume of full cylinder with the given dimensions using the formula.

Volume of full cylinder
`=\pi r^(2) h=\pi* 8^(2) *9=576\pi cm^(3)`

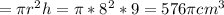
Volume of half cylinder
`=(576\pi )/(2) =288\pi cm^(3)`

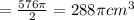
Step 2: Let x be the number of minutes of filling the sand.

`6 cm^(3)` of sand filled every 15 seconds, there are four 15 seconds in a minute.

So volume of sand filled in 1 minute
`= 6*4 cm^(3) = 24 cm^(3)`.

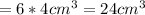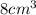`8 cm^(3)` of sand taken out of cylindrical vase every minute.

Net volume of sand filled in 1 minute = Volume of sand filled in the vase in one minute - Volume of sand taken out in 1 minute

Net volume of sand filled in 1 minute
`=24 cm^(3) - 8cm^(3)=16cm^(3)`

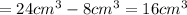
Volume of sand filled in x minutes
`= 16x`.

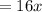We need to set up an equation to find the number of minutes need to fill half the volume in cylindrical vase.

`16x = 288\pi \\ \\ x=(288\pi)/(16) \\ \\ x=18\pi \\ \\ x=57 minutes`

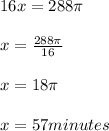
Conclusion:

The number of minutes required for the base be half filled with sand is 57