Question

ΔHAT is similar to ΔCAN.

What is the value of y?

3
7
2
3
(please help)

Answer 1

In similar triangles, the ratios of corresponding sides are equal.

This means

y/6=5/(4+5)

Cross multiply

y=5*6/(4+5)=30/9=10/3 (or 3 1/3)

Answer 2

The value of y is
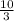`(10)/(3)`. It can be written as
`3(1)/(3)`.

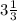Explanation:

It is given that ΔHAT is similar to ΔCAN. The corresponding sides of similar triangle are proportional.

Since ΔHAT is similar to ΔCAN, therefore

`(CN)/(HT)=(AC)/(AH)`

`(CN)/(HT)=(AC)/(AC+CH)`

`(y)/(6)=(5)/(5+4)`

`(y)/(6)=(5)/(9)`

`y* 9=5* 6`

`y* 9=30`

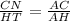
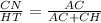
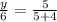
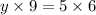
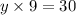
Divide both sides by 9.

`y=(30)/(9)`

`y=(10)/(3)`

`y=3(1)/(3)`

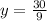
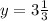
Therefore the value of y is
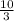`(10)/(3)`. It can be written as
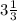`3(1)/(3)`.