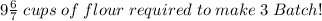Question

5. A certain recipe requires 3 2/7 cups of flour and 2 3/5 cups of sugar. a) If 5/9 of the recipe is to be made, how much sugar is needed? b) If the above ingredients are required for one batch, find the amount of flour needed for a triple batch.

Answer 1

Given:

1 recipe requires
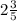`2(3)/(5)` cups of Sugar

1 recipe requires
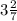`3(2)/(7)` cups of Flour

In the same way,

1 Batch requires
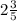`2(3)/(5)` cups of Sugar

1 Batch requires
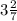`3(2)/(7)` cups of Flour

Solution:

If 1 recipe requires
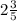`2(3)/(5)` cups of Sugar, to find how much of sugar requires for
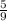`(5)/(9)` recipe, we need to multiply them as below

`(5)/(9) \; recipe \; requires\; \; (5)/(9)\; \cdot\; 2(3)/(5) \; cups \; of\; sugar\\ \\ (5)/(9)\; \cdot\; 2(3)/(5)=(5)/(9)\; \cdot\; (13)/(5)\\\\ Multiply \; numerator \; with \; numerator\; and\; denominator\; with \; denominator \\ \\ (5 \cdot 13 )/(9 \cdot 5) \\ \\ Cancel \; common \; factors \; to \; simplify \; the\; fraction\; to\; its\; lowest\; terms\\ \\ (13)/(9)\\ \\ Rewrite \; it \; as\; mixed\; fraction\\1(4)/(9)`

---

If 1 Batch requires
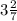`3(2)/(7)` cups of Flour, to find how much of Flour requires for triple Batch, we need to multiply them as below:

`Triple \; Batch \; requires\; \; 3 * 3(2)/(7) \; Cups\; \; of\; \; Flour\\ \\ 3 * 3(2)/(7)\\ Convert \; mixed \; fraction\; to\; improper\; fraction\\ \\ 3 * (23)/(7) \\ Rewrite\; 3\; whole\; number\; as\; a\; fraction\\ \\ (3)/(1) *(23)/(7) \\ Multiply\; numerator\; with\; numerator\; and\; denominator\; with\; denominator\\ \\ (69)/(7)`

`Rewrite\; the\; above \; mixed\; fraction\; to\; improper\; fraction\\ \\ (69)/(7) =9(6)/(7)`

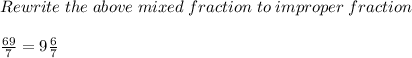
Conclusion:

Part a)

`1(4)/(9) \; cups \; of\; sugar\; required\; to\; make\; 5/9 \; Recipe!`

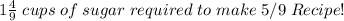
Part b)

`9(6)/(7) \; cups \; of\; flour\; required\; to\; make\; 3 \; Batch!`