The path of the ball is given by
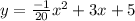 where y is the height in feet and x is the horizontal distance in feet.
where y is the height in feet and x is the horizontal distance in feet.
We will use the second derivative test which states,
If a function has a critical point for which f′(x) = 0 and the second derivative is positive at this point, then f has a local minimum. If, the function has a critical point for which f′(x) = 0 and the second derivative is negative at this point, then f has local maximum.
Firstly, we will calculate the first derivative of the given function,
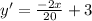
To find the horizontal distance, let y'=0

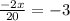
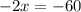
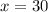
Now let us consider the second derivative of the given function,
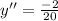
Since the second derivative that is y'' is negative.
Therefore, x=30 is the maximum horizontal distance.
Substituting x =30 in the given function to get the maximum height,
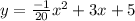
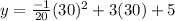
y=50 is the maximum height in feet.