To find the solutions to the system, we need to find exactly when one expression is equal to the other. We can do this by setting both of the right sides equal to each other, so that

Subtracting x+6 from either side, we find
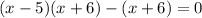
factoring out an x+6:
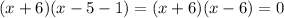

The x-coordinates of our solutions will therefore be 6 and -6. Since the question only asks for the x-coordinate of the midpoint, we simply need to find the number exactly halfway between 6 and -6, which is 0.