What's the answer and why?

Question

asked May 10, 2019 24.8k views

2 Answers

Ecmanaut · Answer 1 · 2019-05-13T21:20:28+0000

The distance
on the map is the hypothenuse of a right triangle whose legs are 5 and 9. To find it, you can use Pythagorean theorem:

d = √(25+81) = √(106)

On the other hand, since 45 minutes are 0.75 hours, driving this amount of time at 30 miles per hour makes you travel

$0.75 \cdot 30 = 22.5$ miles.

So, you have that 22.5 miles correspond to
√(106) centimeters. This means that one centimeter corresponds to

$(22.5)/(√(106)) \approx 2.18539\ldots$

So the closer answer is D

Anton Dovzhenko · Answer 2 · 2019-05-17T01:52:58+0000

check the picture below.

so we can use the pythagorean theorem to get the dashed line of the road,

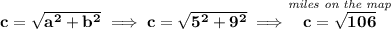
$\bf c=√(a^2+b^2)\implies c=√(5^2+9^2)\implies \stackrel{\textit{miles on the map}}{c=√(106)}$

we know that Sam doing 30mph, can do that road in 45 minutes, in actual length, well, 45 minutes is 3/4 of an hour, so

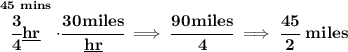
$\bf \stackrel{45~mins}{\cfrac{3}{4}\underline{hr}}\cdot \cfrac{30miles}{\underline{hr}}\implies \cfrac{90miles}{4}\implies \cfrac{45}{2}~miles$

so, that's how many actual miles the road really is, so if we put that in actual : map ratio, we'd get

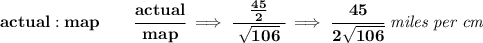
$\bf actual:map\qquad \cfrac{actual}{map}\implies \cfrac{\quad (45)/(2)\quad }{√(106)}\implies \cfrac{45}{2√(106)}\textit{ miles per cm}$

and you know what that is.