So firstly, you want to get rid of the outermost powers. The rule with powering something with an exponent is to multiply the exponents together.
In this case:
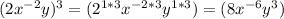 and
and

Our current equation look like this:
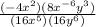
Next, you want to multiply what's on the numerators and the denominator. The rule with multiplying exponents of the same base is to add them together.
In this case:
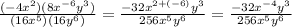
Now we can divide. The rule with dividing exponents with the same base is that you subtract them.
In this case:

Now, if you're required to leave no negative exponents, the rule is that for example x^-2 would turn into 1/x^2. In this case, it would turn like this:
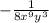 . And that would be your final answer.
. And that would be your final answer.