Answer: The required area of the given equilateral triangle is 20.78 ft².
Step-by-step explanation: We are given to find the area of the equilateral triangle shown in the figure.
We know that the area of an equilateral triangle having radius of circumscribed circle equal to r units is given by
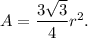
For the given equilateral triangle, we have
r = 4 ft.
Therefore, the area of the given equilateral triangle is
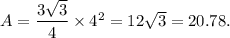
Thus, the required area of the given equilateral triangle is 20.78 ft².