Question

Which graph correctly represents the relationship between arc length and the measure of the corresponding central angle on a circle with radius r?

Answer 1

Answer C for Plato

Explanation:

Based on the explanation above

Answer 2

Please note that the options for the graphs are missing in the question posted. However, I will try my best to answer the question as there is just one graph that is possible.

Please find the two attached diagrams to get a better understanding of the answer provided here.

Let us consider the first diagram. Here, we have a circle with center O. The radius of the circle is
`r`. Let the length of the arc be
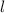`l` and it subtends an angle
`\theta` at the centre.

Now, we know that the relationship between arc length,
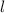`l`, radius,
`r` and angle subtended
`\theta` is given as:

`l=r* \theta=r \theta`

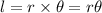
Thus, the relationship is linear and the graph between
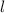`l` and
`\theta` for a given
`r` will be a straight line whose slope will be given by
`r`.

Now, we also know that the maximum arc length that a circle can possibly have is the circumference of the circle which is given by
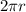`2\pi r` and that happens when the angle
`\theta` subtended at the center is equal to
`2\pi`.

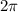Keeping the information of the above two paragraphs please have a look at the second diagram.

This second diagram is the required graph as asked in the question.