Question

The length of the top of a table is 3 m greater than the width. The area is 70 m^2. Find the dimensions of the table.

Answer 1

The final answer is 7 and 10! :)

Answer 2

Let's call the width
`x`. Since the length is three more than the width, it is
`x+3`.

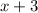The area (which we know to be 70) is given by the multiplication of width and length:

`x(x+3) = 70 \iff x^2+3x = 70 \iff x^2+3x-70 = 0`

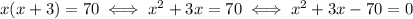
To solve this equation, you can use the usual quadratic formula: given an equation
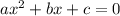`ax^2+bx+c=0`, the two solutions are

`x_(1,2) = (-b\pm√(b^2-4ac))/(2a)`

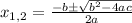
which in your case becomes

`x_(1,2) = (-3\pm√(9+280))/(2) = (-3\pm 17)/(2)`

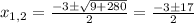
So, two solutions are

`(-3-17)/(20) = -10,\qquad (-3+17)/(2) = 7`

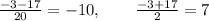
Since we can't accept a negative length, we only accept the second solution.

So, the dimensions are 7 and 10