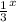The function is y =
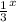
This can be found by using the base equation for exponential y =
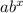 . Now we can use the second ordered pair (0, 1) to find the value of a.
. Now we can use the second ordered pair (0, 1) to find the value of a.
y =
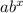
1 =
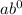
1 = a(1)
1 = a
Now that we have a, we can solve for b using any other ordered pair.
y =
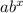
 =
=
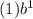
 = (1)(b)
= (1)(b)
 = b
= b
Now we can use these in the same equation.
y =