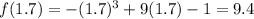General Idea:
In order to find the local extrema of a function f(x), we need to do the below steps:
(i) Find the first derivative of the given function
(ii) Set the first derivative to zero and solve for x to identify the critical numbers.
(iii) Draw a number line plotting the critical numbers in it, then pick a test point from each of the intervals to check whether the function is increasing or decreasing.
(iv) If
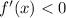 , then function f(x) Decreasing in that interval. If
, then function f(x) Decreasing in that interval. If
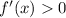 , then the function f(x) Increasing in that interval. Based on this information we can identify the local extrema's.
, then the function f(x) Increasing in that interval. Based on this information we can identify the local extrema's.
Applying the concept:
Given function
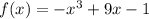
Step 1: Finding the derivative of the function:
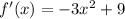
Step 2: Set the
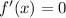 and solve for x to get the critical numbers.
and solve for x to get the critical numbers.
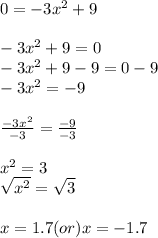
Step 3: We need write the intervals based on the critical numbers
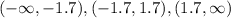
Let us pick a Test point from the interval
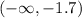 as -2
as -2
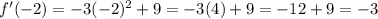
The function will be decreasing in the interval
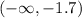
Let us pick a Test point from the interval
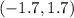 as 0
as 0
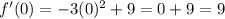
The function will be increasing in the interval
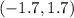
Let us pick a Test point from the interval
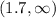 as 2
as 2

The function will be decreasing in the interval
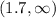 .
.
Conclusion:
At
 , function has a local minimum
, function has a local minimum
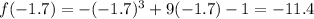
At
 , function has a local maximum
, function has a local maximum