Question

Suppose that U is an infinite universal set, and A and B are infinite subsets of U . Answer the following questions with a brief explanation. Must A c be finite? Must A ∪ B be infinite? Must A ∩ B be infinite?

Answer 1

A c must not be finite.

A ∪ B must be infinite.

A ∩ B must not be infinite.

Explanation:

Must A c be finite?

Suppose

U = {....-4,-3,-2,-1,0,1,2,3,4.......}

A = {....-4,-2,0,2,4.......} which is infinite set

B = {....-3,-1,0,1,3.......} which is also infinite set

So We need to calculate the A compliment

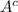`A^(c)` = U - A = {....-4,-3,-2,-1,0,1,2,3,4.......} - {....-4,-2,0,2,4.......} = {....-3,-1,0,1,3.......}

Hence
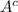`A^(c)` is also an infinite set.

The statement "Must A c be finite?" is incorrect.

Must A ∪ B be infinite?

In AUB all the elements of set A and set B are combined into a single set to get the union of A and B. If A and B are the infinite set then their union must also be an infinite set because all the elements of infinite sets will be there so the union of these infinite sets will also be an infinite set.

The Statement "Must A ∪ B be infinite?" is correct.

Must A ∩ B be infinite?

In A∩B the common elements of both sets will be the answer to the intersection of A and B set. If we consider the A and B are the infinite subsets of a Universal set that carry all the elements then there will not be any common element in both sets A and B.

The Answer of A∩B is { } or empty set.

The statement "Must A ∩ B be infinite? " is incorrect.