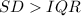Question:
Find the mean and compare it with the median. Find the standard deviation and compare it with the interquartile range. Calculate s for the data 4, 1, 3, 10, 2.
Answer:
(a)

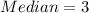
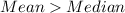
(b)
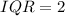
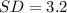
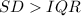
Explanation:
Given:
Data: 4, 1, 3, 10, 2.
Solving (a): The mean and the Median
The mean is calculated as follows:
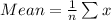
Where
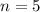 i.e 5 data
i.e 5 data
So, the expression becomes:



Calculating the Median:
First, arrange the order (ascending order):
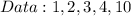
Because n is odd
The median is represented as:


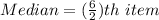

From the arranged data, the 3rd item is 3.
Hence:
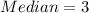
By comparison, the mean is greater than the median because

Solving (b): Standard Deviation and IQR
The standard deviation is calculated as follows:
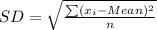
So, we have:

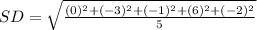
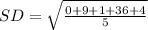

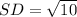
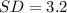
Calculating IQR
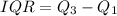
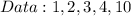
In (a), we calculate the median as:
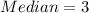
First, we calculate
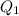
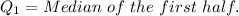
The first half is:
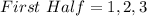
So:

First, we calculate
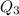

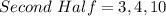
So:

Recall that:
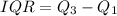
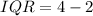
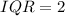
So, we have:
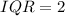
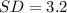
By comparison, the standard deviation is greater than the IQR because:
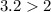
So,