General Idea:
In an arithmetic sequence, to find the
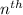 term, we need to use the below formula:
term, we need to use the below formula:

Here
 gives the
gives the
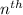 term
term
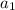 gives the first term of sequence
gives the first term of sequence
d is the common difference and n is the number of terms in the sequence.
Applying the concept:
In our problem it is given that "A company gives each new salesperson a commission of $300 for the sale of a new car",
so
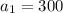
"The salesperson will receive a $100 increase for each addition car the person sells that week"
so
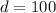
"find the number of cars a salesperson must sell to earn $4,200 in a week", this means that we need to find the value of n, when

Setting up the equation based on the arithmetic sequence formula, we get:
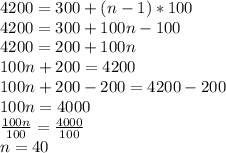
Conclusion:
New Salesperson has to sell 40 cars to earn $4200 in a week.