Question

The sum of the squares of 3 consecutive positive integers is 110. What are the numbers? Which of the following equations is used in the process of solving this problem?

A. 3n^2 + 5 = 110

B.3n^2 + 3n + 3 = 110

C. 3n^2 + 6n + 5 = 110

Answer 1

`n^2 + (n+1)^2 + (n+2)^2 = 110`

`n^2 + n^2 + 2n + 1 + n^2 + 4n + 4 = 110`

`3n^2 + 6n + 5 = 100`

Answer: Choice C

Answer 2

The numbers are 5, 6, 7 and the equation used in the process of solving this problem is
`3n^(2)+6n+5=110`

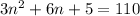
Explanation:

Part a: Which of the following equations is used in the process of solving this problem?

You can use n to represent the first number because the statement says that the numbers are consecutive, we can say that the second number is represented by n+1 and the third by n+2.

Next, we need the squares of the numbers so,
`n^(2) , (n+1)^(2), (n+2)^(2)`.

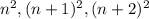And the last step is the sum of the squares to be equal to 110
`n^(2)+(n+1)^(2)+(n+2)^(2)=110`.

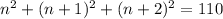To find the equation, we expand and simplify the expression
`n^(2)+(n+1)^(2)+(n+2)^(2)=110\\ n^(2)+n^(2)+2n+1+n^(2)+4n+4=110\\ 3n^(2)+6n+5=110`

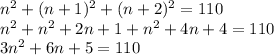
So the equation used in the process of solving this problem is
`3n^(2)+6n+5=110`

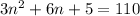
Part b: What are the numbers?

We solve the equation
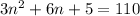`3n^(2)+6n+5=110` using the quadratic formula.

`3n^(2)+6n-105=0\\ x_(1,2) =\frac{-b\±\sqrt{b^(2)-4ac} }{2a}\\ x_(1)= \frac{-6+\sqrt{6^(2)-4*3*-105} }{2*3}, x_(2)= \frac{-6-\sqrt{6^(2)-4*3*-105} }{2*3}\\ x_(1)=5, x_(2)=-7`

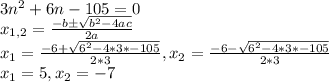
We cannot use
`x_(2)=-7` because the problem says positive integers.

So the numbers are n=5, n+1=6, n+2=7