Question

In a normal respiratory cycle the volume of air that moves into and out of the lungs is about 498 mL. The reserve and residual volumes of air that remain in the lungs occupy about 1990 mL and a single respiratory cycle for an average human takes about 4 seconds. Find a model for the total volume of air V(t) in the lungs as a function of time.

Answer 1

The model is
`V(t)=2239+249\sin((\pi)/(2)t)`.

Explanation:

Consider the given information.

The volume of air inside the lungs increases or decreases so for this we will use the basic sine function
`B(t)=d+a\sin[b(t+ (c)/(a))]` as our parent function.

Let us assume that the phase shift is 0 it means
`(c)/(b)=0`.

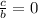The air that moves into and out of the lungs is about 498 mL.

It means the amplitude of the function will vary by 249(half of 498).

The reserve and residual volumes of air that remains in the lungs occupy about 1990 mL which is the minimum air in the lungs.

So, the max air will be: 1990+498 =2488 mL

And the average will be d=1990+249=2239 ml

The horizontal stretch will be
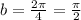`b=(2\pi)/(4)=(\pi)/(2)` as we know that period of
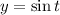`y=\sin t` is
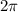`2\pi` and respiratory cycle for an average human takes about 4 seconds.

Hence, the model is
`V(t)=2239+249\sin((\pi)/(2)t)`.