Question

What is the amplitude and period of the following function?


`j(x)=6sin((1)/(3)x)`
Where does this function hit the x-axis?

Answer 1

Hello!

Amplitude is the maximum displacement on the graph of a function.

Period is the displacement of x at which the graph of a function begins to repeat.

We can find the period of a circular function by using the formula:
`P = (2\pi)/(B)`.

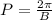The amplitude is 6 because it causes the displacement of the graph to change. Therefore, the domain becomes -6 ≥ x ≥ 6.

To find the period, we use the formula
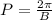`P = (2\pi)/(B)`, and we substitute the values into the equation. The value B, is 1/3.

`P = (2\pi)/((1)/(3))`

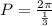
This can be simplified into 6π.

Since the periodicity is 6π, the graph hits the x-axis at intervals of 3π and -3π, and the graph also hits the x-axis at the origin.

Therefore, the amplitude of the function is 6, the period is 6π, and the function hits the x-axis during intervals of 3π.