You can see the three diagram attached. Each link is labeled with the probability: you have probability 1/6 that a six is rolled, and 5/6 that it is not rolled.
To answer the questions, find the path that brings you to the desired outcome, and multiply all the labels you meet.
First question:
To get three sixes, you have to choose the left path at each roll. The probability is always 1/6, so the answer is
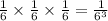
Second question:
To get no sixes, you have to choose the right path at each roll. The probability is always 5/6, so the answer is
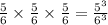
Third question:
To get exactly one six, it can either be the first, second or third roll.
In all cases, you have to choose the left path once and the right path twice: left-right-right mean that you get the six in the first roll, right-left-right means that you get the six in the second roll, right-right-left means that you get the six in the third roll.
In every case, the left turn has probability 1/6, and the right turn has probability 5/6. The probability of each combination is thus

And since there are three of these combinations, The answer is

Fourth question:
Since the question suggests to use what we already achieved, let's do it: having at least one six is the complementary event of having no sixes at all. If an event has probability p, its complementary has probability 1-p. So, since the probability of no sixes is known, the probability of at least one six is
