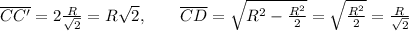Question

Find the rectangle of largest area that can be inscribed in a semicircle of radius R, assuming that one side of the rectangle lies of the diameter of the semicircle.

What is the length of the smaller side of the rectangle?
What is the length of the larger side of the rectangle?

Answer 1

Please refer to the attached figure.

If the circle has radius
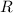`R`, the semicircle has equation
`y = √(R^2-x^2)`, defined for
`-R < x < R`.

The coordinates of the points are:

`C' = (x,0)`

`C = (-x,0)`

`D = (-x,√(R^2-x^2))`

`E = (x,√(R^2-x^2))`

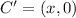
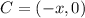
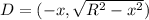
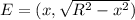
This implies that

`\overline{CC'} = 2x,\qquad \overline{CD} = √(R^2-x^2)`

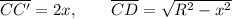
So, the area of the rectangle is the product of the width and the height. We want to find the maximum of

`f(x) = 2x√(R^2-x^2)`

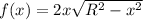
To do so, let's start by computing its derivative:

`f'(x) = 2√(R^2-x^2) + 2x (-2x)/(2√(R^2-x^2)) = 2√(R^2-x^2) - (4x^2)/(√(R^2-x^2)) = (2(R^2-2x^2))/(√(R^2-x^2))`

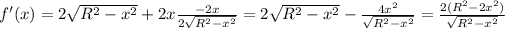
The derivative equals zero if the numerator equals zero:

`2(R^2-2x^2) = 0 \iff R^2-2x^2 = 0 \iff x^2 = (R^2)/(2) \iff x = (R)/(√(2))`

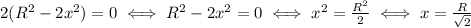
So, we have

`\overline{CC'} = 2(R)/(√(2)) = R√(2),\qquad \overline{CD} = \sqrt{R^2-(R^2)/(2)} = \sqrt{(R^2)/(2)} = (R)/(√(2))`