Question

A firecracker reaches a height of h feet before it bursts. The height h is modeled by h = −16t2 + vt + c, where v is the initial velocity, and c is the beginning height of the firecracker above the ground. The firecracker is placed on the roof of a building of height 15 feet and is fired at an initial velocity of 100 feet per second. Will it reach a height of 100 feet before it bursts? Identify the correct explanation for your answer.

Answer 1

General Idea:

If we have a quadratic function of the form f(x)=ax^{2} +bx+c , then the function will attain its maximum value only if a < 0 & its maximum value will be at x=-\frac{b}{2a} .

Applying the concept:

The height h is modeled by h = −16t^2 + vt + c, where v is the initial velocity, and c is the beginning height of the firecracker above the ground. The firecracker is placed on the roof of a building of height 15 feet and is fired at an initial velocity of 100 feet per second. Substituting 15 for c and 100 for v, we get the function as
`h=-16t^2+100t+15`.

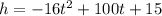Comparing the function f(x)=ax^{2} +bx+c with the given function
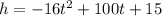`h=-16t^(2) +100t+15`, we get
`a = -16`,
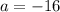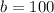`b = 100` and
`c=15`.

The maximum height of the soccer ball will occur at t=\frac{-b}{2a}=\frac{-100}{2(-16)} = \frac{-100}{-32}=3.125 seconds

The maximum height is found by substituting
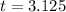`t=3.125` in the function as below:

`h=-16(3.125)^2+100(3.125)+15=171.25 feet`

Conclusion:

Yes ! The firecracker reaches a height of 100 feet before it bursts.