Question

The graph of an equation is shown below:

line joining ordered pairs negative 2, negative 3 and 2,3


Based on the graph, which of the following represents a solution to the equation?


A (−2,−3)


B (2, 1)


C (1, 2)


D (−3, −2)





Answer 1

only (a) is the solution of the graph.

Explanation:

Given : The graph of an equation is shown line joining ordered pairs (-2,-3) and (2,3).

We have to find out of the given options which represents a solution to the equation.

To find which represents a solution to the equation we first find the equation of line

General equation of line is y = mx + c , where m is slope of line and c is y- intercept.

Slope of line m is calculated as
`m=(y_2-y_1)/(x_2-x_1)`

Thus, slope of given line is

`(x_1,y_1)=(-2,-3)\\\\(x_2,y_2)=(2,3)`

Then slope is
`m=(3-(-3))/(2-(-2))=(3)/(2)`

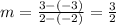
Thus, slope of line is
`m=(3)/(2)`,

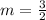Equation becomes,

`y=(3)/(2)x+c`

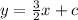
On solving, we get,

`2y=3x+2c`

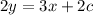
To find c , Put (2,3) in Equation 2y = 3x + 2c , we get,

⇒ 2(3) = 3(2) + 2c

⇒ 6 = 6 + 2c

⇒ c = 0

Thus, equation of line is
`y=(3)/(2)x`.

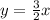Now we plot the graph of the equation, we get as attached and check those points lies on the equation are the solution.

Thus, only (a) is the solution of the graph.

Answer 2

`(-2,-3)`

Explanation:

Let

`A(-2,-3), B(2,3)`

Find the slope of the line

The formula to calculate the slope between two points is equal to

`m=(y2-y1)/(x2-x1)`

substitute the values

`m=(3+3)/(2+2)`

`m=(6)/(4)`

`m=1.5`

Find the equation of the line

`y-y1=m(x-x1)`

With m and the point A

`y+3=1.5(x+2)`

`y=1.5x`

If a ordered pair is a solution of the linear equation, then the ordered pair must be satisfy the linear equation

case A)
`(-2,-3)`

Is a solution because represent the point A

Substitute the values of x and y in the linear equation

`-3=1.5(-2)`

`-3=-3` ------> the ordered pair is a solution of the linear equation

case B)
`(2,1)`

Substitute the values of x and y in the linear equation

`1=1.5(2)`

`1\\eq 3` ------> the ordered pair is not a solution of the linear equation

case C)
`(1,2)`

Substitute the values of x and y in the linear equation

`2=1.5(1)`

`2\\eq 1.5` ------> the ordered pair is not a solution of the linear equation

case D)
`(-3,-2)`

Substitute the values of x and y in the linear equation

`-2=1.5(-3)`

`-2\\eq -4.5` ------> the ordered pair is not a solution of the linear equation