Question

NEED HELP HERE PLEASE.

6.06



Solve the triangle.


A = 33°, a = 20, b = 13 (1 point)




Cannot be solved


B = 20.7°, C = 146.3°, c ≈ 23.7


B = 20.7°, C = 126.3°, c ≈ 17.8


B = 20.7°, C = 126.3°, c ≈ 29.6



2. State whether the given measurements determine zero, one, or two triangles.


C = 30°, a = 32, c = 16 (1 point)




Two


Zero


One



3. Two triangles can be formed with the given information. Use the Law of Sines to solve the triangles.


A = 59°, a = 13, b = 14 (1 point)




B = 22.6°, C = 98.4°, c = 15; B = 157.4°, C = 81.6°, c = 15


B = 67.4°, C = 53.6°, c = 13.8; B = 112.6°, C = 8.4°, c = 13.8


B = 22.6°, C = 98.4°, c = 11.3; B = 157.4°, C = 81.6°, c = 11.3


B = 67.4°, C = 53.6°, c = 12.2; B = 112.

Answer 1

1. Solve the triangle. A = 33°, a = 20, b = 13 (1 point)

`(a)/(\sin A) = (b)/(\sin B)`

`\sin B = (b)/(a) \sin A= (13)/(20) \sin 33 \approx 0.3540`

`B = \arcsin .3540 = 20.73^\circ`

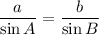
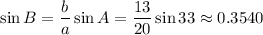
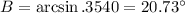
The supplement of B (which has the same sine) is around 159° so with A exceeds 180 degrees so we ignore it.

`C = 180^\circ - A - B = 180 - 33 - 20.73 = 126.27^\circ`

`c = (\sin C)/(\sin A ) a= (\sin 126.27)/(\sin 33) (20) \approx 29.6`

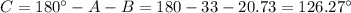
Fourth choice: B = 20.7°, C = 126.3°, c ≈ 29.6

2. State whether the given measurements determine zero, one, or two triangles. C = 30°, a = 32, c = 16 (1 point)

`\sin A = (a)/(c) \sin C= (32)/(16) \sin 30 = 2(\frac 1 2)=1`

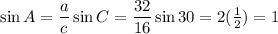
That's unique, A=90°

One triangle.

3. Two triangles can be formed with the given information. Use the Law of Sines to solve the triangles. A = 59°, a = 13, b = 14 (1 point)

`\sin B = (b)/(a) \sin A= (14)/(13) \sin 59 \approx 0.9231`

There are two triangle angles with this sine, supplementary to each other,

`B_1 \approx 67.4 \textrm{ or } B_2 \approx 180- 67.4 = 112.6`

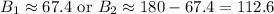
Since when combined with A=59° neither A+B exceeds 180°, we have two valid triangles.

`C_1 = 180 - 59 - 67.4 = 53.6`

`c_1 = (\sin C_1)/(\sin A ) a = (\sin 53.6)/(\sin 59) (13) = 12.2`

`C_2 = 180 - 59 - 112.6 = 8.4`

`c_2 = (\sin C_2)/(\sin A ) a = (\sin 8.4)/(\sin 59) (13) = 2.2`

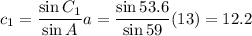
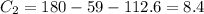
That's the last choice, suitably edited:

B = 67.4°, C = 53.6°, c = 12.2; B = 112.6°, C = 8.4°, c = 2.2