Question

It takes 40 min for a bus to cover 36 miles. A car travels 1.4 times faster. When will they meet if they started 36 miles apart and simultaneously move towards each other?

Answer 1

Let's get a big picture view of what we want to find in this problem. It wants to know when the car and the bus meet, given they're traveling towards each other. To get this in terms of numbers, we want to know how much time has passed when the distance between them is 0. Our unknown - what we want to find - is how much time has passed when that happens. There's another way we could look at this, though. The question says that the car and the bus start 36 miles apart - the moment they're 0 miles apart is the same moment they've traveled 36 miles between them.

In other words, adding the distance traveled by the car and the distance traveled by the bus should get us exactly 36 miles. If we call the car's distance
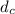`d_c` and the bus's distance
`d_b`:

`d_c+d_b=36`

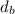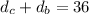
To find the distance each vehicle travels, we can multiply the speed they're traveling at by the amount of time they've been travelling. We'll call the time traveled t, and we'll measure it in minutes. We'll also call the speed of the car
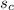`s_c` and the speed of the bus
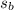`s_b`. This makes their distances

`d_b=s_bt \\d_c=s_ct`

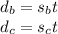
There's some other key information we can use to help us, though. We know that the car travels 1.4 times as fast as the bus, which means it travels 1.4 times as far in the same time. Mathematically, we can write this

`d_c=1.4d_b`

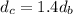
This simplifies the equation at the center of our focus, which we can rewrite now as

`1.4d_b+d_b=36\\2.4d_b=36\\d_b=15`

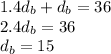
substituting our earlier formula for
`d_b`:

`s_bt=15`

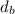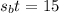
since t is what we're looking for, we want to get it by itself, which we can do by dividing both side of the equation by
`s_b`:

`t=(15)/(s_b)`

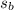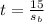
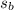`s_b`, the bus's speed in miles per minute, is actually given in the question; it covers 36 miles in 40 minutes, or 36/40 = 9/10 miles per minute, so
`s_b=(9)/(10)`.

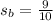Plugging that value in, we find

`t = 15 / (9)/(10)=15*(10)/(9) =(50)/(3) =16(2)/(3)`

So, it takes 16 2/3 minutes, or 16 minutes and 40 seconds for the two vehicles to meet.

Answer 2

Bus:

40 min = 36 miles

1 min = 36 ÷ 40 = 0.9 mile

Car:

1 min = 0.9 x 1.4 = 1.26 miles

Total distance covered by both vehicles in 1 min:

1.26 + 0.9 = 2.16 miles

Time needed for both of them to cover 36km:

36 ÷ 2.16 = 16 2/3 min

Answer: They will meet 16 2/3 mins after they have started.