Question

An arithmetic sequence has this recursive formula:

What is the explicit formula for this sequence?

Answer 1

The answer is A. an=8+(n-1)(-6) .

Explanation:

Answer 2

Hello!

The recursive rule for an arithmetic sequence:
`a_(n) = a_(n-1) + d`.

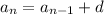The explicit rule for an arithmetic sequence:
`a_(n)=a_(1) +d(n-1)`.

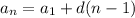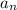`a_(n)` is the value you are trying to find, or simply the answer. :)

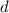`d` is the common difference of the sequence.

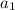`a_(1)` is the first term of the sequence.

Given,
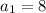`a_(1) = 8` and
`a_(n)=a_(n-1) - 6`...

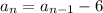The common difference is -6, and the first term is 8.

Plug these values into the explicit rule for an arithmetic sequence, you get:

`a_(n)=8+(-6)(n-1)`.

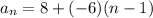Therefore, the answer is A,
`a_(n)=8+(n-1)(-6)`.

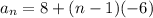If you wondered why,
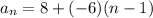`a_(n)=8+(-6)(n-1)` is equal to
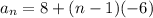`a_(n)=8+(n-1)(-6)`, the Commutative Property of Multiplication states that when two numbers are multiplied together, the answer is the same regardless of the order of the numbers, which makes
`a_(n)=8+(-6)(n-1)` and
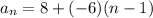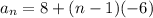`a_(n)=8+(n-1)(-6)` equal to each other.