Answer:
Option B is correct.
The ASA congruence postulates or theorem proves that △ABC and △CDA are congruent.
Step-by-step explanation:
Angle Side Angle (ASA) theorems states that if two angles and the included side of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent.
In △ABC and △CDA
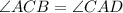 [Angle] [Given]
[Angle] [Given]
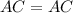 [Side] [Reflexive property]
[Side] [Reflexive property]
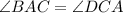 [Angle] [Given]
[Angle] [Given]
Then, by the ASA theorem;
