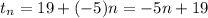Arithmetic sequences are generated by taking some initial term and continually adding or subtracting a constant term from it. What this means is that the differences between neighboring pairs of terms will always be the same - that difference gives us our constant term.
The first sequence contains the terms 17, 22, 27, 32, etc. Taking the differences of the neighboring pairs, we find that 22 - 17 = 27 - 22 = 32 - 27 = 5. If we start with 12 and add 5 once, we get 17; if we add 5 twice, we get 22, and so on. Written out in equation form:
17 = 12 + 5(1)
22 = 12 + 5(2)
27 = 12 + 5(3)
and in general,
 .
.
In the second sequence, we obtain each following term by subtracting 5 from the previous one, which has the same effect as adding -5. We add -5 to 19 once to get 14, twice to get 9, etc. Again, in equation form, that's
14 = 19 + (-5)(1)
9 = 19 + (-5)(2)
4 = 19 + (-5)(3)
and in general,