Question

Need help asap with 1 math question, please help. Offering double the points!

Answer 1

It’s the second one
Hope this helps!!

Answer 2

So firstly, we have to figure out what the vertex is. The best method of doing this is by converting the standard form equation to vertex form.

First step is to separate x^2-4x and 12 with parentheses:
`y=(x^2-4x)+12`

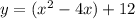
Next, to make what's inside the parentheses a perfect square, we want to find what is half of the x coefficient and then square that. In this case, that is four. Add 4 inside of the parentheses, and add -4 outside of the parentheses:
`y=(x^2-4x+4)+12-4`

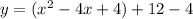
Next, you want to factor (x^2-4x+4), which is (x-2)^2, and combine 12 and -4 together, and your vertex form is
`y=(x-2)^2+8`

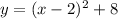
Now that we have the vertex form, we can find the vertex. To find this, if the vertex form was
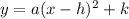`y=a(x-h)^2+k` , then the vertex is (h,k). In this context, h = 2 and k = 8, therefore your vertex is (2,8) and the table with that vertex is the fourth table.